25-03-2025 - Chemistry Basics - Thermodynamics (part 6), entropy variations [EN]-[IT]
6 comments

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
25-03-2025 - Chemistry Basics - Thermodynamics (part 6), entropy variations [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_68)
Thermodynamics (part 6), entropy variations

Image created with artificial intelligence. The software used is Microsoft Copilot
Relationship between entropy variation and heat exchanged
To better understand the relationship between entropy variation and heat exchanged, we must rely on the formulation of the second law through the Clausius inequality. Essentially, the second law of thermodynamics describes the behavior of thermal systems. This principle establishes fundamental limits for energy transformations.

Within this principle lies one of the most well-known formulations known as the Clausius inequality. In reversible thermodynamic processes, studies carried out on thermodynamic systems have a low complexity. We absolutely cannot say the same thing about systems, or rather irreversible thermodynamic processes. The Clausius inequality provides the mathematical condition for understanding irreversible thermodynamic processes. Essentially, this inequality establishes a relationship between the heat exchanged by a system and the temperature at which this heat is transferred. What this inequality states is that for reversible processes, i.e. ideal processes, without dissipation, or internal resistances, the integral is equal to zero, while for irreversible processes, i.e. practically all real processes, the integral is less than zero.
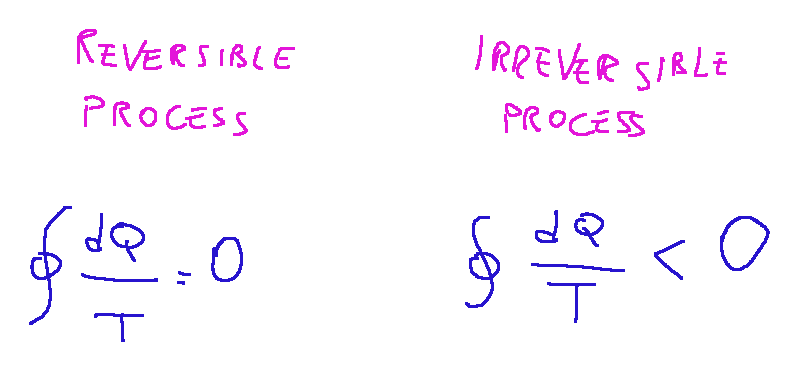
Basically the important thing that this mathematical formula tells us is that in an irreversible process the entropy of the system increases which means that the disorder of an irreversible system increases.
Exercise
Heat is not a state function. What do you have to multiply it by to make it so?
Heat (described in the formulas above with the letter Q) is not a state function. This means that it depends on the variation that will occur to get from one state to another. So it does not only depend on the initial and final states.
We know that entropy is defined as the ratio between the heat exchanged and the temperature.
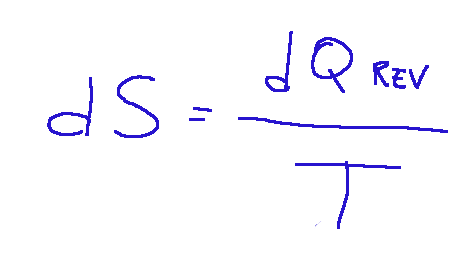
This shows that when you divide heat by temperature, you get a state function, namely entropy, which is independent of the path of the process.
If we multiply heat by the reciprocal of temperature, we get a quantity that depends only on the initial and final states of the system, making this quantity a state function.
Note:
A thermodynamic quantity:
-is a state function if its value depends only on the current state of the system, and not on the path that the system has followed to arrive at that state.
-is not a state function if the value depends on the way in which the system was brought from the initial state to the final state.
Conclusions
In conclusion we can say that from the Clausius inequality we can understand that natural processes tend to increase disorder (entropy). We can deduce that in an isolated system it is not possible to realize a thermodynamic process in which all the thermal energy is transformed into work without having losses.
Question
A heat engine that converts all the heat into work can be defined as a perfect machine. Did you know that the various thermodynamic studies on entropy definitively declare that a perfect heat engine cannot exist in the world?

[ITALIAN]
25-03-2025 - Basi di chimica - Termodinamica (part 6), variazioni di entropia [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_68)
Termodinamica (part 6), variazioni di entropia

Immagine creata con l'intelligenza artificiale. Il software usato è Microsoft Copilot
Legame tra variazione di entropia e calore scambiato
Per comprendere meglio il legame tra la variazione di entropia ed il calore scambiato, dobbiamo aggrapparci alla formulazione del secondo principio mediante la disuguaglianza di Clausius. Sostanzialmente il secondo principio della termodinamica descrive il comportamento dei sistemi termici. Questo principio stabilisce limiti fondamentali per le trasformazioni energetiche.

All’interno di questo principio risiede una delle formulazioni più conosciute che è nota come la disuguaglianza di Clausius. Nei processi termodinamici reversibili gli studi effettuati sui sistemi termodinamici hanno una bassa complessità. Non possiamo assolutamente dire la stessa cosa dei sistemi, o meglio dei processi termodinamici irreversibili. La disuguaglianza di Clausius fornisce la condizione matematica per comprendere i processi termodinamici irreversibili. Sostanzialmente questa disuguaglianza stabilisce una relazione tra il calore scambiato da un sistema e la temperatura alla quale questo calore viene trasferito. Quello che afferma questa disuguaglianza è che per i processi reversibili, cioè processi ideali, senza dissipazione, o resistenze interne, l’integrale è uguale a zero, mentre per i processi irreversibili, quindi praticamente tutti i processi reali, l’integrale è minore di zero.
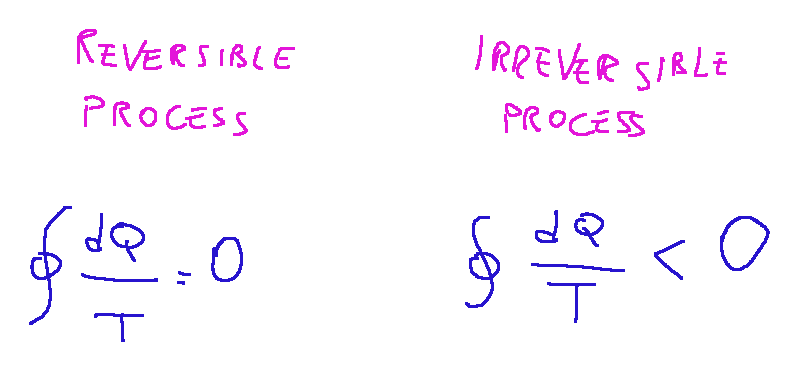
Praticamente la cosa importante che ci dice questa formula matematica è che in un processo irreversibile l’entropia del sistema aumenta il che significa che il disordine di un sistema irreversibile aumenta.
Esercizio
Il calore non è una funzione di stato. Per cosa bisogna moltiplicarlo per renderlo tale?
Il calore (descritto nelle formule qui sopra riportate con la lettera Q) non è una funzione di stato. Questo vuol dire che dipende dalla variazione che ci sarà per arrivare da uno stato all'altro. Quindi non dipende solo dallo stato iniziale e da quello finale.
Sappiamo che l'entropia è definita il rapporto tra il calore scambiato e la temperatura.
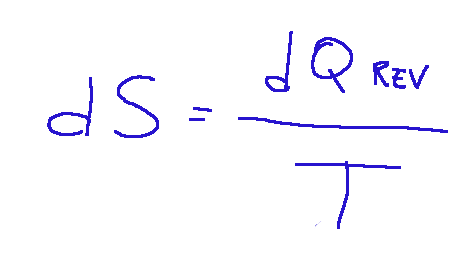
Questo dimostra che, quando si divide il calore per la temperatura, si ottiene una funzione di stato, cioè l'entropia, la quale è indipendente dal percorso del processo.
Se moltiplichiamo il calore per il reciproco della temperatura, otteniamo una quantità che dipende solo dallo stato iniziale e dallo stato finale del sistema, rendendo tale grandezza una funzione di stato.
Nota:
Una grandezza termodinamica:
-è una funzione di stato se il suo valore dipende solo dallo stato attuale del sistema, e non dal percorso che il sistema ha seguito per arrivare a quello stato.
-non è una funzione di stato se il valore dipende dal modo in cui il sistema è stato portato dallo stato iniziale a quello finale.
Conclusioni
In conclusione possiamo dire che dalla disuguaglianza di Clausius possiamo comprendere che i processi naturali tendono ad aumentare il disordine (l'entropia). Possiamo dedurre che in un sistema isolato non è possibile realizzare un processo termodinamico in cui tutta l'energia termica venga trasformata in lavoro senza avere delle perdite.
Domanda
Un motore termico che converta tutto il calore in lavoro può essere definito come una macchina perfetta. Sapevate che i vari studi termodinamici sull'entropia dichiarano in maniera definitiva che al mondo non può esistere una macchina termica perfetta?
THE END

Comments