Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

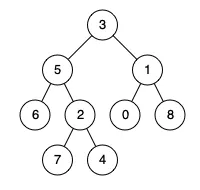
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

Constraints:

• The number of nodes in the tree is in the range [2, 105].
• -109 <= Node.val <= 109
• All Node.val are unique.
• p != q
• p and q will exist in the tree.

🤓Explanation

Okay, imagine you’re trying to find a common ancestor for two people in a family tree. The “lowest common ancestor” is like the closest shared grandparent or great-grandparent they have.

Here’s how you can think about finding it in a tree-like structure (like a family tree or a computer tree):

The Problem: Given a big family tree (the root) and two specific people in that tree (person A and person B), find the closest shared ancestor.

The Idea: We’ll start at the top of the tree and work our way down. For each person we look at, we’ll ask:

• “Is this person one of the two people we’re looking for?” If yes, then this person could be the lowest common ancestor (especially if the other person is in their family line below).
• “Are both of our target people in the family line below this person, but on different sides?” If yes, then this person we’re currently looking at is the lowest common ancestor. They’re the first one who has both of them as descendants in separate branches.
• “Are both of our target people in the family line below this person, but on the same side?” If yes, then we need to continue our search down that same side. The lowest common ancestor must be further down.
• “Is only one of our target people (or none) in the family line below this person?” If only one is found, then that person (if it’s the current one we’re checking) might be the ancestor. If neither is found below, then this branch isn’t helpful.

function findLowestCommonAncestor(tree_node, person_A, person_B):
  if tree_node is empty OR tree_node is person_A OR tree_node is person_B:
    return tree_node  // We found one of the people or reached the end

  found_in_left_branch = findLowestCommonAncestor(tree_node's left child, person_A, person_B)
  found_in_right_branch = findLowestCommonAncestor(tree_node's right child, person_A, person_B)

  if found_in_left_branch is NOT empty AND found_in_right_branch is NOT empty:
    return tree_node // We found one person on each side, so the current node is the LCA

  // Otherwise, the LCA must be in the branch where we found someone (or it's the person we found)
  if found_in_left_branch is NOT empty:
    return found_in_left_branch
  else:
    return found_in_right_branch

In Simple Terms

Imagine you’re looking for where two cousins’ family lines first meet going up the family tree. You start at a common ancestor (maybe way up high).

• If you find one of the cousins, that might be the meeting point, or you need to keep looking in their branch for the other cousin.
• If you find one cousin’s line going left and the other cousin’s line going right from a specific ancestor, then that ancestor is the first one they share.
• If both cousins’ lines are on the same side (say, both go left), then you need to continue looking further down that left side to find their first shared ancestor.

This process continues until you find the “lowest” (closest) ancestor that both people are descendants of.

The found targets bubble upwards. This is the cornerstone of our Boolean logic, we can do this because the problem assumes both p and q exists within the tree.

Implementations

🐍Python

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        """
        Finds the lowest common ancestor (LCA) of two nodes in a binary tree.

        The LCA is defined as the lowest node in the tree that has both p and q as descendants
        (where we allow a node to be a descendant of itself).

        Args:
            root (TreeNode): The root node of the binary tree.
            p (TreeNode): The first node.
            q (TreeNode): The second node.

        Returns:
            TreeNode: The lowest common ancestor node of p and q.
        """
        # Base case: If the current root is None, or if the current root is one of the target nodes (p or q),
        # then this root is either the LCA (if the other target is in its subtree) or part of the path to the LCA.
        if not root or root == p or root == q:
            return root

        # Recursively search for the LCA in the left subtree.
        left = self.lowestCommonAncestor(root.left, p, q)

        # Recursively search for the LCA in the right subtree.
        right = self.lowestCommonAncestor(root.right, p, q)

        # If the left subtree search returns a non-None node and the right subtree search also returns a non-None node,
        # it means that p is found in one subtree and q is found in the other. Therefore, the current root is the LCA.
        if left and right:
            return root

        # If only one of the recursive calls returned a non-None node, it means that either:
        # 1. Both p and q are in that subtree, and the returned node is their LCA.
        # 2. One of p or q is the returned node (from the base case), and the other is in its subtree (which would have been handled in the 'left and right' case if both were found).
        # So, we return the non-None result (either 'left' or 'right').
        return left or right

🟦Typescript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

/**
 * Finds the lowest common ancestor (LCA) of two nodes in a binary tree.
 *
 * The LCA is defined as the lowest node in the tree that has both `p` and `q` as descendants
 * (where we allow a node to be a descendant of itself).
 *
 * @param root The root node of the binary tree.
 * @param p The first node.
 * @param q The second node.
 * @returns The lowest common ancestor node of `p` and `q`, or `null` if `root` is `null`.
 */
function lowestCommonAncestor(root: TreeNode | null, p: TreeNode | null, q: TreeNode | null): TreeNode | null {
    // Base case: If the current root is null, or if the current root is either p or q,
    // then this root is either the LCA (if it's p or q and the other is in its subtree)
    // or part of the path to the LCA.
    if (!root || root === p || root === q) {
        return root;
    }

    // Recursively find the LCA in the left subtree.
    const left = lowestCommonAncestor(root.left, p, q);

    // Recursively find the LCA in the right subtree.
    const right = lowestCommonAncestor(root.right, p, q);

    // If both left and right recursive calls return a non-null node, it means that p is found
    // in one subtree and q is found in the other. Therefore, the current root is the LCA.
    if (left && right) {
        return root;
    }

    // If only one of the recursive calls returned a non-null node, it means that either:
    // 1. Both p and q are in that subtree, and the returned node is their LCA.
    // 2. One of p or q is the returned node (from the base case), and the other is in its subtree (which would have been handled in the 'left && right' case if both were found).
    // So, we return the non-null result (either 'left' or 'right').
    return left || right;
}

🦀Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//     pub val: i32,
//     pub left: Option<Rc<RefCell<TreeNode>>>,
//     pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//     #[inline]
//     pub fn new(val: i32) -> Self {
//         TreeNode {
//             val,
//             left: None,
//             right: None
//         }
//     }
// }
use std::rc::Rc;
use std::cell::RefCell;

impl Solution {
    /// Finds the lowest common ancestor (LCA) of two nodes in a binary tree.
    ///
    /// The LCA is defined as the lowest node in the tree that has both `p` and `q` as descendants
    /// (where we allow a node to be a descendant of itself).
    ///
    /// # Arguments
    ///
    /// * `root`: An `Option` containing an `Rc<RefCell<TreeNode>>` which is the root node of the binary tree.
    /// * `p`: An `Option` containing an `Rc<RefCell<TreeNode>>` which is the first node.
    /// * `q`: An `Option` containing an `Rc<RefCell<TreeNode>>` which is the second node.
    ///
    /// # Returns
    ///
    /// An `Option` containing an `Rc<RefCell<TreeNode>>` which is the lowest common ancestor node of `p` and `q`.
    pub fn lowest_common_ancestor(root: Option<Rc<RefCell<TreeNode>>>, p: Option<Rc<RefCell<TreeNode>>>, q: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
        // Base case: If the current root is None, return None.
        if root.is_none() {
            return None;
        }

        // Borrow the inner TreeNode from the Rc<RefCell<TreeNode>> for easier access to its fields.
        let root_ref = root.as_ref().unwrap().borrow();
        let p_ref = p.as_ref().unwrap().borrow();
        let q_ref = q.as_ref().unwrap().borrow();

        // If the current root is one of the target nodes (p or q), then this root is either the LCA
        // (if the other target is in its subtree) or part of the path to the LCA.
        // We use Rc::ptr_eq to compare the actual memory addresses of the nodes.
        if Rc::ptr_eq(root.as_ref().unwrap(), p.as_ref().unwrap()) || Rc::ptr_eq(root.as_ref().unwrap(), q.as_ref().unwrap()) {
            return root.clone();
        }

        // Recursively search for the LCA in the left subtree.
        let left_lca = Self::lowest_common_ancestor(root_ref.left.clone(), p.clone(), q.clone());

        // Recursively search for the LCA in the right subtree.
        let right_lca = Self::lowest_common_ancestor(root_ref.right.clone(), p.clone(), q.clone());

        // If the left subtree search returns a non-None node and the right subtree search also returns a non-None node,
        // it means that p is found in one subtree and q is found in the other. Therefore, the current root is the LCA.
        if left_lca.is_some() && right_lca.is_some() {
            return root.clone();
        }

        // If only the left subtree search returned a non-None node, it means that both p and q (or one of them)
        // are in the left subtree, and the 'left_lca' node is their LCA.
        if left_lca.is_some() {
            return left_lca;
        }

        // If only the right subtree search returned a non-None node (and the 'left_lca' check failed), it means that
        // both p and q (or one of them) are in the right subtree, and the 'right_lca' node is their LCA.
        return right_lca;
    }
}

---

If you liked this content I’d appreciate an upvote or a comment. That helps me improve the quality of my posts as well as getting to know more about you, my dear reader.

Muchas gracias!

Follow me for more content like this.

X | PeakD | Rumble | YouTube | Linked In | GitHub | PayPal.me | Medium

Down below you can find other ways to tip my work.

BankTransfer: "710969000019398639", // CLABE
BAT: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875",
ETH: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875",
BTC: "33xxUWU5kjcPk1Kr9ucn9tQXd2DbQ1b9tE",
ADA: "addr1q9l3y73e82hhwfr49eu0fkjw34w9s406wnln7rk9m4ky5fag8akgnwf3y4r2uzqf00rw0pvsucql0pqkzag5n450facq8vwr5e",
DOT: "1rRDzfMLPi88RixTeVc2beA5h2Q3z1K1Uk3kqqyej7nWPNf",
DOGE: "DRph8GEwGccvBWCe4wEQsWsTvQvsEH4QKH",
DAI: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875"