Source: Leetcode.com

Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.

Return the number of good nodes in the binary tree.

Example 1:

Input: root = [3,1,4,3,null,1,5]
Output: 4
Explanation: Nodes in blue are good.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.

Example 2:

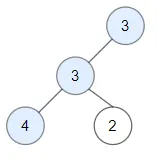
Input: root = [3,3,null,4,2]
Output: 3
Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.

Example 3:

Input: root = [1]
Output: 1
Explanation: Root is considered as good.

Constraints:

• The number of nodes in the binary tree is in the range [1, 10^5].
• Each node’s value is between [-10^4, 10^4].

Explanation

Okay, imagine you have a special tree made of building blocks. Each block has a number on it. Some blocks are higher up in the tree (closer to the top), and some are lower down.

We want to count how many “good” blocks there are. A block is “good” if its number is the biggest number you’ve seen so far on the way down from the very top of the tree to that block.

🌲Overall Plan:

1. Start at the very top block (the root).
2. Keep track of the biggest number we’ve seen on our way down.
3. For each block we visit:

• Check if the number on this block is bigger than or the same as the biggest number we’ve seen so far.
• If it is, then this block is “good”! We count it.
• Remember that this block’s number is now the biggest number we’ve seen for the blocks below it.

4 - Go down the left side of the tree and do the same thing.
5 - Go down the right side of the tree and do the same thing.
6 - Keep doing this until we’ve looked at all the blocks.
7 -The total number of “good” blocks we counted is our answer!

✏️Example with Pseudocode

Let’s say our tree looks like this (imagine circles are blocks with numbers):

      (5)  <-- Top block
     /   \
   (3)     (8)
  / \     /
(1) (4) (9)

Let’s walk through it:

1. We start at the top block with the number 5. This is the first block, so the biggest number we’ve seen so far is 5 (or even a super tiny number before we started, so 5 is definitely bigger!). So, 5 is a good block! Our count of good blocks is now 1.
2. Now we go to the left block with the number 3. The biggest number we saw on the way here was 5. Is 3 bigger than or the same as 5? No! So, 3 is not a good block. But, for the blocks below 3, the biggest number we’ve seen on their way down from the top is still 5 (because 3 wasn’t bigger).
3. From 3, we go to the left block with the number 1. The biggest number we saw on the way here was 5. Is 1 bigger than or the same as 5? No! So, 1 is not good.
4. From 3, we go to the right block with the number 4. The biggest number we saw on the way here was 5. Is 4 bigger than or the same as 5? No! So, 4 is not good.
5. Now we go back to the top (5) and go to the right block with the number 8. The biggest number we saw on the way here was 5. Is 8 bigger than or the same as 5? Yes! So, 8 is a good block! Our count is now 2. For the blocks below 8, the biggest number we’ve seen on their way down is now 8.
6. From 8, we go to the left block with the number 9. The biggest number we saw on the way here was 8. Is 9 bigger than or the same as 8? Yes! So, 9 is a good block! Our count is now 3.

We’ve looked at all the blocks. The total number of good blocks we counted is 3 (the blocks with numbers 5, 8, and 9).

function countGoodBlocks(topBlock):
  goodCount = 0

  function checkBlock(currentBlock, biggestNumberSoFar):
    if currentBlock is empty (no block here):
      return

    if currentBlock.number is bigger or same as biggestNumberSoFar:
      goodCount = goodCount + 1
      newBiggestNumber = currentBlock.number
    else:
      newBiggestNumber = biggestNumberSoFar

    checkBlock(currentBlock.left, newBiggestNumber)
    checkBlock(currentBlock.right, newBiggestNumber)

  checkBlock(topBlock, a very small number like -infinity)
  return goodCount

In the real computer code, we use something called “recursion” to do the “go left and go right” steps again and again until we reach the end of each branch of the tree. And we keep passing along the biggest number we’ve seen so far!

Implementations

🐍Python

# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def goodNodes(self, root: TreeNode) -> int:
        """
        Counts the number of "good" nodes in a binary tree.

        A node is considered "good" if the value of the node is greater than or
        equal to the maximum value on the path from the root to that node.

        Args:
            root (TreeNode): The root node of the binary tree.

        Returns:
            int: The total number of good nodes in the tree.
        """
        self.good_nodes_count = 0  # Initialize the counter for good nodes

        def traverse(node: Optional[TreeNode], greatest_value_so_far: int):
            """
            Recursively traverses the binary tree and checks for good nodes.

            Args:
                node (Optional[TreeNode]): The current node being visited.
                greatest_value_so_far (int): The maximum value encountered on the
                                             path from the root to the current node.
            """
            _greatest_value_so_far = greatest_value_so_far  # Create a local copy

            if not node:
                return  # Base case: if the node is None, stop recursion

            # Check if the current node is a good node
            if node.val >= greatest_value_so_far:
                self.good_nodes_count += 1  # Increment the count of good nodes
                _greatest_value_so_far = node.val  # Update the greatest value seen so far

            # Recursively traverse the left and right subtrees
            if node.left:
                traverse(node.left, _greatest_value_so_far)
            if node.right:
                traverse(node.right, _greatest_value_so_far)

        # Initiate the traversal starting from the root with negative infinity as the
        # initial greatest value (ensuring the root is always considered good)
        traverse(root, float('-inf'))

        return self.good_nodes_count

🟦Typescript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 * val: number
 * left: TreeNode | null
 * right: TreeNode | null
 * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 * this.val = (val===undefined ? 0 : val)
 * this.left = (left===undefined ? null : left)
 * this.right = (right===undefined ? null : right)
 * }
 * }
 */

function goodNodes(root: TreeNode | null): number {
    let goodNodesCount: number = 0;

    function traverse(node: TreeNode | null, greatestValueSoFar: number): void {
        let _greatestValueSoFar: number = greatestValueSoFar;

        if (!node) {
            return;
        }

        if (node.val >= greatestValueSoFar) {
            goodNodesCount++;
            _greatestValueSoFar = node.val;
        }

        traverse(node.left, _greatestValueSoFar);
        traverse(node.right, _greatestValueSoFar);
    }

    if (root) {
        traverse(root, -Infinity);
    }

    return goodNodesCount;
};

🦀Rust

// // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//     pub val: i32,
//     pub left: Option<Rc<RefCell<TreeNode>>>,
//     pub right: Option<Rc<RefCell<TreeNode>>>,
// }

// impl TreeNode {
//     #[inline]
//     pub fn new(val: i32) -> Self {
//         TreeNode {
//             val,
//             left: None,
//             right: None
//         }
//     }
// }

use std::rc::Rc;
use std::cell::RefCell;

impl Solution {
    /// Counts the number of "good" nodes in a binary tree.
    ///
    /// A node is considered "good" if the value of the node is greater than or
    /// equal to the maximum value on the path from the root to that node.
    ///
    /// # Arguments
    ///
    /// * `root` - An optional reference-counted, mutable-borrowed pointer to the root node of the binary tree.
    ///
    /// # Returns
    ///
    /// The total number of good nodes in the tree.
    pub fn good_nodes(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        /// Recursively traverses the binary tree and checks for good nodes.
        ///
        /// # Arguments
        ///
        /// * `node` - An optional reference-counted, mutable-borrowed pointer to the current node being visited.
        /// * `greatest_value_so_far` - The maximum value encountered on the path from the root to the current node.
        /// * `count` - A mutable reference to the counter for good nodes.
        fn traverse(node: Option<Rc<RefCell<TreeNode>>>, greatest_value_so_far: i32, count: &mut i32) {
            if let Some(node_ref) = node {
                let node_borrow = node_ref.borrow();
                let current_val = node_borrow.val;

                if current_val >= greatest_value_so_far {
                    *count += 1;
                }

                let next_greatest = std::cmp::max(greatest_value_so_far, current_val);

                traverse(node_borrow.left.clone(), next_greatest, count);
                traverse(node_borrow.right.clone(), next_greatest, count);
            }
        }

        let mut good_nodes_count = 0;
        if let Some(r) = root.clone() {
            traverse(Some(r), i32::MIN, &mut good_nodes_count);
        }
        good_nodes_count
    }
}

---

If you liked this content I’d appreciate an upvote or a comment. That helps me improve the quality of my posts as well as getting to know more about you, my dear reader.

Muchas gracias!

Follow me for more content like this.

X | PeakD | Rumble | YouTube | Linked In | GitHub | PayPal.me | Medium

Down below you can find other ways to tip my work.

BankTransfer: "710969000019398639", // CLABE
BAT: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875",
ETH: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875",
BTC: "33xxUWU5kjcPk1Kr9ucn9tQXd2DbQ1b9tE",
ADA: "addr1q9l3y73e82hhwfr49eu0fkjw34w9s406wnln7rk9m4ky5fag8akgnwf3y4r2uzqf00rw0pvsucql0pqkzag5n450facq8vwr5e",
DOT: "1rRDzfMLPi88RixTeVc2beA5h2Q3z1K1Uk3kqqyej7nWPNf",
DOGE: "DRph8GEwGccvBWCe4wEQsWsTvQvsEH4QKH",
DAI: "0x33CD7770d3235F97e5A8a96D5F21766DbB08c875"